Extras: Rotation Matrix
This page is a prerequisite sort of thing for math used throughout the other stuff.
I. Rotation Matrix
Rotation matrices are a fun thing that make a point go from one place to another based on an axis and a rotation angle. Look at this diagram to see what I mean:
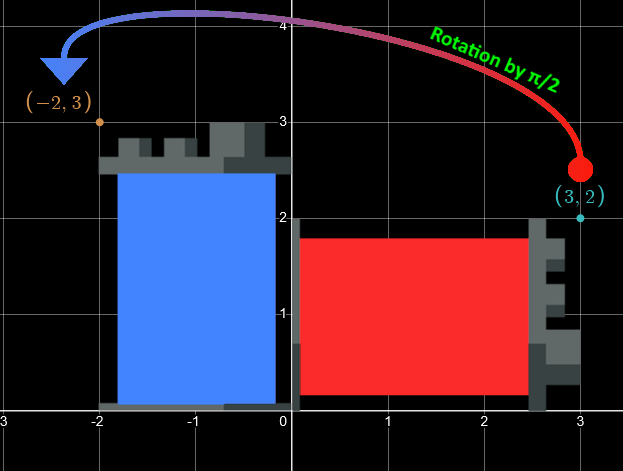
What I've done is visualized the rotation using a building. The red building is the initial position (3,2). After a rotation by π/2, we arrive at the
coordinate (-2,3). This is done using the rotation matrix:
(Wikimedia)
Or rather,
X' = X * cos(angle) - Y * sin(angle) and Y' = X * sin(angle) + Y * cos(angle).
II. Sin and Cos Basics
Sin and Cos are two trigonometric functions that, when you're dealing with circles, are the best way to do stuff. It's not too complex: just think of a circle with a radius of 1, aka a unit circle. Now take any angle (in radians) that starts pointing at (1,0) and then goes counterclockwise. Sin will return the Y value while Cos will return the X value.

