Part B: The Swirling Gases
Note: Before diving in, check out Part A: The Smoke Pillar for context.
This guide lays out the mathematical setup for creating a mushroom cloud. Let’s get swirling.
A mushroom cloud consists of two main parts:
- The pillar of smoke (Part A).
- The swirling gases (Part B).
This page is all about Part B; the swirly gas vortex thingy.
Math Time
WARNING: High levels of BS trig and circle math ahead. You have been warned.
Alright, time to model the swirly gases. Here’s a diagram to visualize what we’re dealing with:
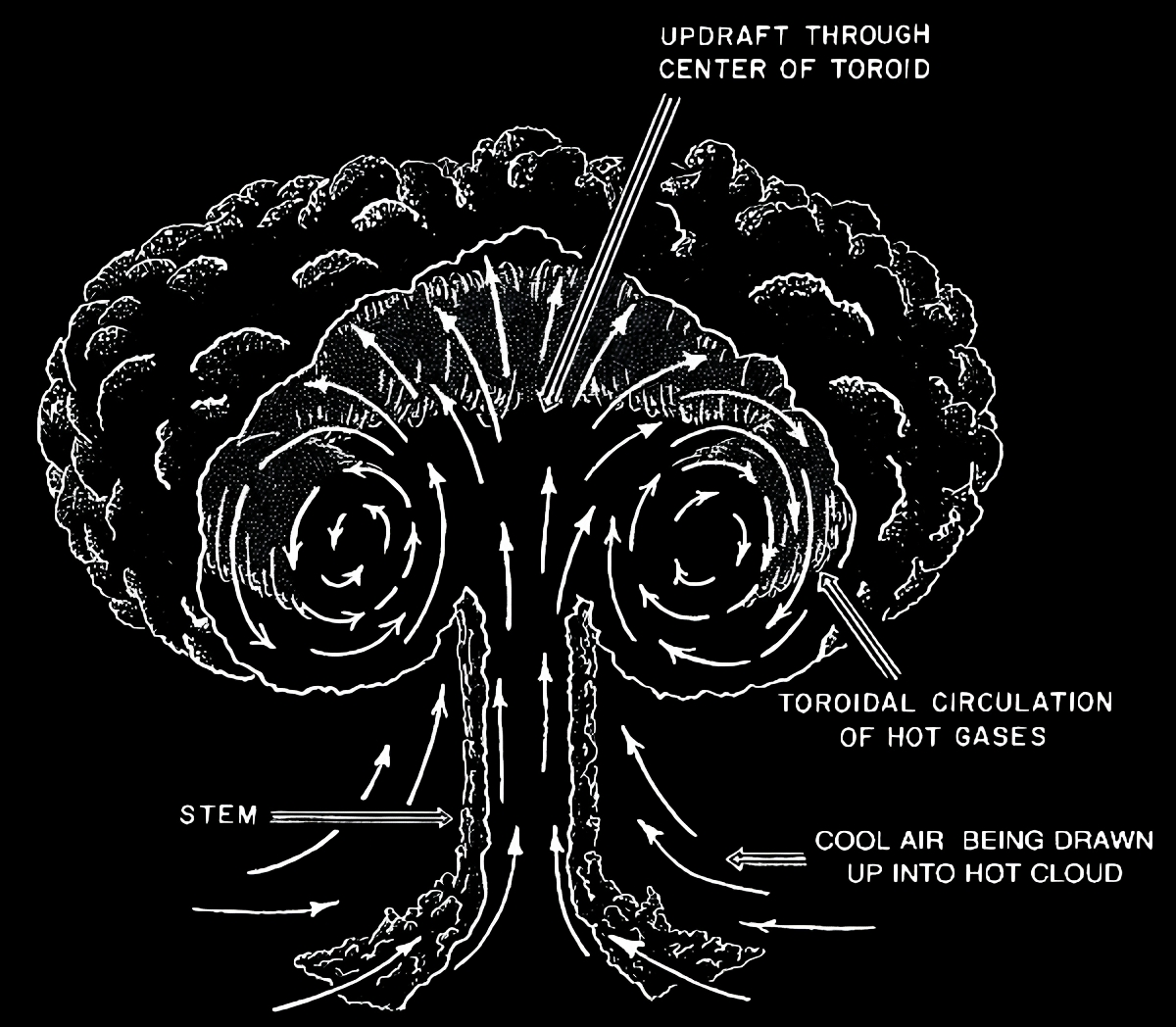
We use sine and cosine to calculate how much each particle moves. And since describing math with words alone is painful, here’s more diagrams. Hooray!
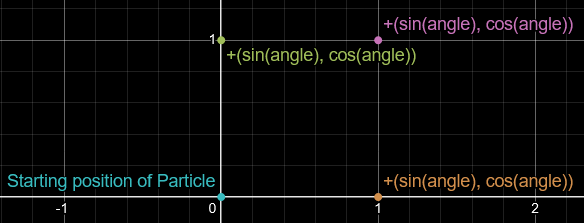
By shifting a particle by (sin(angle), cos(angle)) as angle increases, we get a loop. At first, it looks more like a square than a circle, but don’t panic, we can just decrease the angle increment. Also, if you’re wondering why X is offset by sin and Y by cos (instead of the usual way), it’s so the particles move outward and then back in, meeting at a single point (which we can later tweak into a torus!).
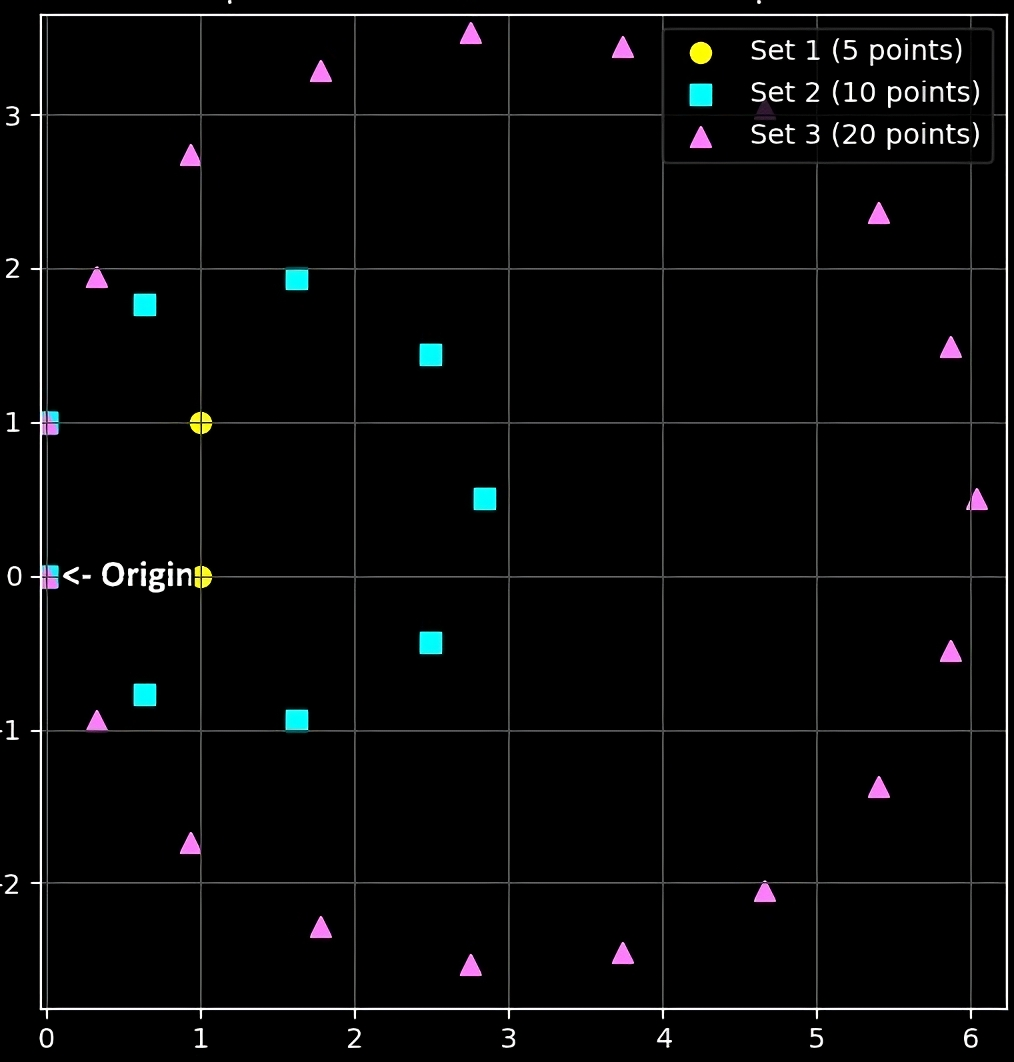
Here’s what different increment values look like. Each set has one less visible point than labeled due to the 0→2π loop. More points = smoother circle.
In Minecraft, if you call super.tick() before displacement, it smooths out movement, so even Set 2 will look like it has way more than 10 points.
Also, the more points you add, the bigger the circle gets. This happens because P' = P + (sin(angle), cos(angle)), and a smaller increment moves P' farther.
You could "fix" this with ratios or something fancy, but honestly, just test it in-game. Too big? Divide the displacement value. Too small? Multiply it.
Math is constant, but art is a process. You’ll have to tweak things. I highly recommend adding dev commands to adjust radius values live in-game, it'll save you from the dreaded
'Close Game -> Change Variable -> Open Game -> Test -> Repeat'.
Now this is a lot of confusing math, so if you learn by example or by good ol' copy-paste, here you go:
public void partB() {
swirlAngle += swirlIncrement;
if (swirlAngle >= 2 * Math.PI) swirlAngle -= 2 * Math.PI;
float rStart, rEnd, gStart, gEnd, bStart, bEnd;
if (swirlAngle < Math.PI) {
rStart = 255; rEnd = 115;
gStart = 75; gEnd = 115;
bStart = 0; bEnd = 115;
} else {
rStart = 125; rEnd = 255;
gStart = 115; gEnd = 75;
bStart = 115; bEnd = 0;
}
float progress = (float) ((swirlAngle % Math.PI) / Math.PI);
this.rCol = Math2.interpolateColor(rStart,rEnd,progress);
this.gCol = Math2.interpolateColor(gStart,gEnd,progress);
this.bCol = Math2.interpolateColor(bStart,bEnd,progress);
double verticalMovement = Math.cos(swirlAngle) * swirlRadius;
double horizontalMovement = Math.sin(swirlAngle) * swirlRadius * 1.5;
localY += verticalMovement;
localZ += horizontalMovement;
double relativeX = localX - originX;
double relativeY = localY - originY;
double relativeZ = localZ - originZ;
Vector2D rotatedXZ = Math2.rotateCoordinate2D(relativeX, relativeZ, rotationAngle).offset(offsetX, offsetZ).offset(originX, originZ);
this.setPos(rotatedXZ.x, originY + relativeY, rotatedXZ.y);
}